根据分子运动理论,空气的冷热程度只是一种现象,它实质上是空气内能大小的表现。当空气获得热量时,其内能增加,气温也就升高;反之,空气失去热量时,内能减小,气温也就随之降低。空气内能变化既可由空气与外界有热量交换而引起;也可由外界压力的变化对空气作功,使空气膨胀或压缩而引起。在前一种情况下,空气与外界有热量交换,称为非绝热变化;在后一种情况下,空气与外界没有热量交换,称为绝热变化。
(一)气温的非绝热变化
空气与外界交换热量有如下几种方式,即传导、辐射、对流、湍流和蒸发凝结(包括升华、凝华)。
1.传导
空气是依靠分子的热运动将能量从一个分子传递给另一分子,从而达到热量平衡的传热方式。空气与地面之间,空气团与空气团之间,当有温度差异时,就会以传导方式交换热量。但是地面和大气都是热的不良导体,所以通过这种方式交换的热量很少,其作用仅在贴地气层中较为明显。因在贴地气层中,空气密度大,单位距离内的温度差异也较大。
2.辐射
是物体之间依各自温度以辐射方式交换热量的传热方式。大气主要依靠吸收地面的长波辐射而增热,同时,地面也吸收大气放出的长波辐射,这样它们之间就通过长波辐射的方式不停地交换着热量。空气团之间,也可以通过长波辐射而交换热量。
3.对流
当暖而轻的空气上升时,周围冷而重的空气便下降来补充(图2·18),这种升降运动,称为对流。通过对流,上下层空气互相混合,热量也就随之得到交换,使低层的热量传递到较高的层次。这是对流层中热量交换的重要方式。
4.湍流
空气的不规则运动称为湍流,又称乱流(图2·19)。湍流是在空气层相互之间发生摩擦或空气流过粗糙不平的地面时产生的。有湍流时,相邻空气团之间发生混合,热量也就得到了交换。湍流是摩擦层中热量交换的重要方式。
5.蒸发(升华)和凝结(凝华)
水在蒸发(或冰在升华)时要吸收热量;相反,水汽在凝结(或凝华)时,又会放出潜热。如果蒸发(升华)的水汽,不是在原处凝结(凝华),而是被带到别处去凝结(凝华),就会使热量得到传送。例如,从地面蒸发的水汽,在空中发生凝结时,就把地面的热量传给了空气。因此,通过蒸发(升华)和凝结(凝华),也能使地面和大气之间、空气团与空气团之间发生潜热交换。由于大气中的水汽主要集中在5km以下的气层中,所以这种热量交换主要在对流层下半层起作用。

以上分别讨论了空气与外界交换热量的方式,事实上,同一时间对同一团空气而言,温度的变化常常是几种作用共同引起的。哪个为主,哪个为次,要看具体情况。在地面与空气之间,最主要的是辐射。在气层(气团)之间,主要依靠对流和湍流,其次通过蒸发、凝结过程的潜热出入,进行热量交换。
(二)气温的绝热变化
1.绝热过程与泊松方程
大气中进行的物理过程,通常伴有不同形式的能量转换。在能量转换过程中,空气的状态要发生改变。在气象学上,任一气块与外界之间无热量交换时的状态变化过程,叫做绝热过程。在大气中,作垂直运动的气块,其状态变化通常接近于绝热过程。当升、降气块内部既没有发生水相变化,又没有与外界交换热量的过程,称作干绝热过程。
要求出在绝热过程中气温的变化,必须应用热力学第一定律。如有dQ热量加到一个孤立的气体系统中,该热量可分为两部分,即增加该系统的内能(dE)及对外所作的功(dW)。因此,对于空气,热力学第一定律可以写成
dQ=dE+dW (2·24)
对于理想气体来说,气体内能就是其分子运动的动能。对1g气体而言,它等于CvT(T为气体温度,Cv为定容比热)。当气温变化为dT时,其值为
dE=CvdT (2·25)
(2·24)式右边第二项为在定压状况下气体膨胀时所作的功。如以P表示压力,V表示气体比容,则
dW=PdV (2·26)
将(2·25)、(2·26)式代入(2·24)式,得
dQ=CvdT+PdV (2·27)
利用状态方程PV=RT,对它进行微分,则有
PdV+VdP=RdT (2·28)
将(2·28)式代入(2·27)式,消去PdV,并用CP=CV+R表示气体的定压比热,得
这是气象学中热力学第一定律的常用形式。
式中,dQ为单位质量空气由于热传导、辐射引起的热量变化;CP是空气的定压比热。如果讨论的对象是单位质量的干空气,实测CP=1.005J/(g·K);R为比气体常数,对干空气来说,比气体常数Rd=0.287J/(g·K)。
当系统是绝热变化时,即dQ=0时,其状态的变化,即向外作功是要靠系统内能负担,(2·29)式可写为
上式将气体的压力变化和温度变化联系起来。在大气中,气压变化主要由空气块的位移引起。在绝热条件下,当空气质点上升时,压力减少,dP<0,这时CPdT<0,因而温度要降低;当空气质点下沉时,压力增加,dP>0,这时CPdT>0,因而温度要升高。
对(2·30)式在(P0,P)及(T0,T)范围内积分
(2·32)式是干绝热方程,亦称泊松(Poisson)方程。它给出了干绝热过程气块初态(P0,T0)和终态(P,T)之间的内在联系,即绝热变化时温度随气压变化的具体规律。例如初态为P0=1000hPa,T0=273K,就可以算出气压变为1050hPa时,温度将变为276.7K;当气压变为900hPa时,温度将变为265K。
2.干绝热直减率和湿绝热直减率
气块绝热上升单位距离时的温度降低值,称绝热垂直减温率(简称绝热直减率)。对于干空气和未饱和的湿空气来说,则称干绝热直减率,以γd
对于所讨论的大多数大气过程而言,能够满足准静力条件,即气块的气压Pi,时时都与四周大气的气压P处于平衡,即Pi=P及Pi+dPi=P+dP。又因为
此为静力学基本方程,其中ρ为周围大气的密度。则
再运用状态方程(2·33)式则为
在实际大气中,Ti与T之差通常不超过10度,以绝对温标表示的比值
若忽略g随高度和纬度的微小变化及Cp随温度的微小变化,取g=9.81m/s2,CP=1.005J/(g·K)=1.005×1000gm2/(s2·g·K)=1005m2/(s2·K),以度/100m为γd的单位,则
实际工作中取γd=1℃/100m,这就是说,在干绝热过程中,气块每上升100m,温度约下降1℃。必须注意:γd与γ(气温直减率)的含义是完全不同的。γd是干空气在绝热上升过程中气块本身的降温率,它近似于常数;而γ是表示周围大气的温度随高度的分布情况。大气中随地-气系统之间热量交换的变化,γ可有不同数值,即可以大于、小于或等于γd。
如果气块的起始温度为T0,干绝热上升△Z高度后,其温度T为
T=T0-γd△Z (2·35)
下面来讨论饱和空气绝热变化的情况:饱和湿空气绝热上升时,如果只是膨胀降温,亦应每上升100m减温1℃。但是,水汽既已饱和了,就要因冷却而发生凝结,同时释放凝结潜热,加热气块。所以饱和湿空气绝热上升时因膨胀而引起的减温率恒比干绝热减温率小。饱和湿空气绝热上升的减温率,称为湿绝热直减率,以γm表示。
设1g饱和湿空气中含有水汽qsg,绝热上升,凝结了dqsg水汽,所释放出的潜热为
dQ=-Ldqs (2·36)
式中L表示水汽的凝结潜热。上式右边的负号表示当有水汽凝结时得到热量,因为这时水汽减少,dqs<0,则dQ> 0;当水分蒸发时消耗热量,这时 dqs> 0,则dQ<0。
应用饱和湿空气的热力学第一定律的形式,则为
由于这个方程中只包含湿空气的相变所产生的热量,而没有考虑其它的热量,所以(2·37)式又称为温绝热方程。饱和湿空气上升时,方程(2·37)可写成
上式说明,饱和湿空气上升时,温度随高度的变化是由两种作用引起的:一种是由气压变化引起的,例如上升时气压减小,dP<0,这使得温度降低;另一种作用是由水汽凝结时释放潜热引起的,上升时水汽凝结,dqs<0,造成温度升高。因此,凝结作用可抵消一部分由于气压降低而引起的温度降低。有水汽凝结时,空气上升所引起的降温将比没有水汽凝结时要缓慢。
类似于求干绝热直减率γd的推导,可得
由此,湿绝直减率γm的表达式可写成:
和温度的函数。表2·4给出不同温度和气压下γm的值。由表可见,γm随温度升高和气压减小而减小。这是因为气温高时,空气的饱和水汽含量大,每降温1℃水汽的凝结量比气温低时多。例如,温度从20℃降低到19℃时,每立方米的饱和空气中有1g的水汽凝结;而温度从0℃降到-1℃时,每立方米的饱和空气中只有0.33g的水汽凝结。这就是说饱和空气每上升同样的高度,在温度高时比温度低时能释放出更多的潜热。因此,在气压一定的条件下,高温时空气湿绝热直减率比低温时小一些。
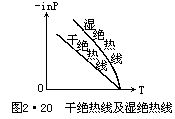
图2·20为干、湿绝热线的比较,干绝热线直减率近于常数,故呈一直线;而湿绝热线,因γm<γd,故在干绝热线的右方,并且下部因为温度高,γm小,上部温度低,γm大,这样形成上陡下缓的一条曲线。到高层水汽凝结愈来愈多,空气中水汽含量便愈来愈少,γm愈来愈和γd值相接近,使干、湿绝热线近于平行。
3.位温和假相当位温
空气块在干绝热过程中,其温度是变化的,同一气块处于不同的气压(高度)时,其温度值常常是不同的,这就给处在不同高度上的两气块进行热状态的比较带来一定困难。为此,假设把气块都按绝热过程移到同一高度(或等压面上),就可以进行比较了。把各层中的气块循着干绝热的程序订正到一个标准高度:1000hPa处,这时所具有的温度称为位温,以θ表示。根据泊松方程,即可得到位温的表达式
式中,T、P分别为干绝热过程起始时刻的温度和气压。从(2·42)式可以看出,位温θ是温度T和气压P的函数。在气象学中,一般常用的热力图表以温度T为横坐标,以压力对数lnP为纵坐标,称为温度对数压力图解。该图上的干绝热线即为等位温线,是根据(2·42)式绘制的。当已知空气的温度和压力时,我们可由热力图表直接读出位温θ来。
显然,气块在循干绝热升降时,其位温是恒定不变的。这是位温的重要性质。
必须指出,位温只是把气块的气压、温度考虑进去的特征量,并且只有在干绝热过程中才具有保守性。在湿绝热过程中,由于有潜热的释放或消耗,位温是变化的。为此,又可导引出把潜热影响考虑进去的温湿特征量。
大气中的水汽达到凝结时,一般是部分凝结物脱离气块而降落,另一部分随气块而运动。为了理解潜热对气块的作用,可假设一种极端的情况,即水汽一经凝结,其凝结物便脱离原上升的气块而降落,而把潜热留在气块中来加热气团,这种过程称假绝热过程。当气块中含有的水汽全部凝结降落时,所释放的潜热,就使原气块的位温提高到了极值,这个数值称为假相当位温,用θse表示,根据定义
式中,q是气块在1000hPa处,1g湿空气所含水汽量
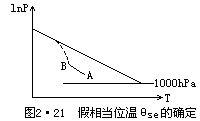
由(2·43)式可以看出θse是气压、温度和湿度的函数。如图2·21所示,设有一气块,其温、压、湿分别为(P、T、q)。在绝热图表上温度、压力始于A点,这时气块是未饱和的,令其沿干绝热线上升到达凝结高度B点,这时气块达到饱和;当气块再继续上升时,就不断地有水汽凝结,这时它将沿湿绝热线上升降温。当气块内水汽全部凝结降落后,再令其沿干绝热线下沉到1000hPa,此时气块的温度就是假相当位温θse。它不仅考虑了气压对温度的影响,而且也考虑了水汽对温度的影响,实际上是关于温度、压力、湿度的综合特征量,对于干绝热、假绝热和湿绝热过程都具有保守性。
以上讨论了大气中空气块温度的绝热变化和非绝热变化。事实上,同一时间对同一团空气而言,温度的变化常常是两种原因共同引起的。何者为主,则要看当时的具体情况。当空气团停留在某地或在地面附近作水平运动时,外界的气压变化很小,但受地面增热和冷却的影响却很大,因而气温的非绝热变化是主要的。空气团作升降运动时,虽然也能和外界交换热量,但因垂直方向上气压的变化很快,空气团因膨胀或压缩引起的温度变化,要比和外界交换热量引起的温度变化大得多,因而气温的绝热变化是主要的。
